那么现在是下半部分,讨论如何用Python来写一个自动化工具,以生成一个初步的LaTeX代码供后续修改完善。
那么,基于之前所提到的内容,实际需要完成的工作有两个部分,其一是生成一个抽象的图,其二是把这个抽象的图表现出来。
第一步,实际上有很多现成的思路可以用,而且也很简单,所以就手撸了一套出来(当然现在再回过头来看有些粗糙了,有很多更好的解决方案,最后再谈)。
第二步,则基本上是对着LaTeX代码拼接字符串了。
那么,这里分步讲。
构造
尽管如此,那么先讲一下当时的思路吧。由于Sankey图本身只是一个点和线构成的有向图,因此需要两个基本的部件 Node 和 Line ,同时每个 Node 有一个在LaTeX中的代号和图上的标签,而 Line 则是有一个起点,一个终点,和流量值,于是有:
class Node:
def __init__(self, name: str, label: str = ""):
self.name = name
self.label = label if label else name和:
class Line:
def __init__(self, source: Node, target: Node, val: float | int):
self.source = source
self.target = target
if val <= 0:
raise ValueError("The value of a Sankey line must be positive.")
self.val = val其中的一些对于输入值的合法性判断就略过不谈了。另外由于笔者的习惯,写这类工具时会开启pylance的类型检查的basic模式并添加类型注释(type hint),所以大概会有很多和算法无关的代码,读者自行忽略即可。
在之后的设计中, Node 和 Line ,特别是 Node ,会作为词典( dictionary )的键,因此需要添加如下两个方法(只举例 Node 的, Line 类似)来使对象成为可哈希的:
def __eq__(self, other: object) -> bool:
if not isinstance(other, Node):
return NotImplemented
return self.name == other.name and self.label == other.label
def __hash__(self) -> int:
return hash((self.name, self.label))另外,由于之后谈到的原因,添加一个复制的方法会很方便,比如:
# under Node
def copy(self) -> 'Node':
return Node(self.name, self.label)
# under Line
def copy(self) -> 'Line':
return Line(self.source.copy(), self.target.copy(), self.val)最后,笔者在设计 Node 类的时候存在一点小失误,没有为 Node 类添加总流量这一属性。当时的考虑是这一属性值并不能在创建 Node 的时候先验的知道,而是需要在图里计算(如果先验的就知道这个值的话,那使用自动化工具与否的总代码量实际也差不多了)。因此如果要添加这个属性,就还要添加两条这个节点的流入线和流出线这两个属性。这样一来 Node 就有些不太“基础”了。但是现在回过头来看,似乎这样的设计反而比较好,也更符合直觉。但这一个小失误总体上损失也不算大,虽然导致后续一处设计有些冗杂,但也降低了后面 SankeyDiagram 这个类的复杂度、减少了各个类之间的联动,只是没法把生成节点的LaTeX代码的函数很优雅地写成 Node 类的方法,有些遗憾了(不会后续改进的时候会想一个优雅的方法加上也说不定)。但是对于 Line 类却显然可以做到:
def latex_repr(self, direction: Literal['to', 'from']) -> str:
if direction == 'to':
return f"{self.val}/{self.source.name}-{direction}-{self.target.name}"
elif direction == 'from':
return f"{self.val}/{self.target.name}-{direction}-{self.source.name}"
else:
raise ValueError("Direction must be either 'to' or 'from'.")那么现在,基本的组件有了,就可以开始构造 SankeyDiagram 这个类了。
一个Sankey图当然由点和线构成,所以基本的有:
class SankeyDiagram:
def __init__(self):
self.nodes: list[Node] = []
self.lines: list[Line] = []
self._diagram: dict[Node, NodeInfo] = {}初始化函数的前两行没什么说的。第三行就是把节点的流出流出信息写到一个词典中。 NodeInfo 是定义的一个 TypedDict ,用于类型检查,可以理解为一个词典类型,定义是:
class NodeInfo(TypedDict):
inflows: list[Line]
outflows: list[Line]这样 self._diagram 的实际结构就类似于:
self._diagram = {Node1: {'inflows': [Line1, Line2, ...],
'outflows': [Line3, Line4, ...]
Node2: {...},
...}}这个属性就存储了所有关于Sankey图的信息。正如之前所说,这里或许应该把这个词典拆开放到 Node 类中。
这个属性用下划线标记成了私有属性,因为给定了节点和有向线,图就已经完成了,不容再手动更改。因此这里定义了一个 diagram 的属性作为外部访问的接口,同时不设置对应的 setter 来设置它的值:
@property
def diagram(self):
if not self._diagram:
self._generate_diagram()
return self._diagram
def _generate_diagram(self):
for node in self.nodes:
self._diagram[node] = {'inflows': [], 'outflows': []}
for line in self.lines:
self._diagram[line.source]['outflows'].append(line)
self._diagram[line.target]['inflows'].append(line)
# check for isolated nodes
for node in self.nodes:
if not self._diagram[node]['inflows'] and not self._diagram[node]['outflows']:
print(f"Warning: Node {node} is isolated and has no inflows or outflows.")
self._diagram.pop(node)
# rearrange the lines based on the reversed node order
reversed_nodes = self.nodes[::-1]
for node in reversed_nodes:
inflows = self._diagram[node]['inflows']
outflows = self._diagram[node]['outflows']
inflows.sort(key=lambda line: reversed_nodes.index(line.source))
outflows.sort(key=lambda line: reversed_nodes.index(line.target))
self._diagram[node]['inflows'] = inflows
self._diagram[node]['outflows'] = outflows这里顺便去掉了孤立的节点并对线进行了排序。排序的原因在于,为了美观起见,我们会希望从一个节点流出或者流入的线不会有交叉,那么在分叉时就要按照“上方的线流向上方的节点,下方的线流向下方的节点”的原则来分配线的位置。什么节点在上方是一个相当任意的选择,这里简单选择了“后添加的节点放在上面”这一条。这样,基于上一篇文章中提到的 \sankeyfork 的语法,就需要“流向后添加的节点的线排在前面”,因此这里用节点的反序来作为线的顺序。当然这里也可以在 sort 中指定顺序来实现而不用先对节点列表反序,就像后面一样,不过是具体实现方式的区别,都用 Python 了就不在乎这点内存了。
那么,到这里为止,整个Sankey图已经构造完成了,接下来就是将它画出来的部分。
绘制
由于线的绘制是LaTeX自己就能搞定的,所以实际上只需要安排好节点的位置、分配好节点的颜色、计算节点流量和做好分叉即可。首先是安排节点位置。上面已经约等于把节点的上下位置排列做好了,下面只需要安排左右位置,所以在类中添加这么一个函数:
def determine_node_x_positions(self) -> dict[Node, int]:这个函数返回一个词典,键是每一个节点,值是这个节点在横向上的位置。只是生成一个模板,不需要考虑很精细的位置调控,因此只需要给出一个 int 就好。
接下来的问题是,横向上怎么排列?简单起见,这里考虑要绘制的Sankey图是一个无环的联通的图。前者是说,不存在从一个节点出来顺流而下又回到这个节点的情况;后者是说,从一个节点出来沿着线逆流或者顺流总能到其他任意一个节点。不考虑有环,是因为笔者的工作中基本不会遇到有环的情况,所以遇到了再说;不考虑非联通,是因为这样为什么不干脆画两张图呢?
那么,在这种简单的情况下,一个自然的想法就是,“同一级”的节点排列在同一个水平位置上,这些节点的纵向位置则按上文所说的那样决定。那么,什么是“同一级”?在这里计算水平位置的时候,实际上计算的是节点之间的相对位置,只需要知道某节点在另一个节点的左边和右边即可,不需要知道绝对的位置,因为完全可以对整张图进行平移来变换到任意的绝对的位置。因此,不妨随便选择一个节点作为水平位置的零点,来考察其他节点相对于它的位置。那么,“同一级”就比较好定义了:沿着这个节点逆流而上的那个节点,就比这个节点低一级;顺流而下的那个节点,就比这个节点高一级。如此递推,就能确定流经这个节点的所有流线上的节点是第几级了。
但似乎还有一个问题,这样递推的话很可能不能遍历每一个节点,就需要再进行多次递推,因此很可能会出现同一个节点被分配到多个级别上。要解决这个问题也很容易,只需要再加一条原则:“相同流向的方向永远相同,反之亦然”,也就是说,比如如果都是从低级的节点向高级的节点流动,那么这些流线一定都是从左到右的,反之亦然。那这样的话,如果分配一个节点的级别时发现这个节点已经被分配过了,那如果当前是在逆流而上地递推,就取这个节点较小的那个级别;如果是顺流而下,就取较大的级别。所以这样,这个方法就可以这么写:
def determine_node_x_positions(self) -> dict[Node, int]:
node_positions: dict[Node, int] = {}
def trace_back(node: Node):
inflows = self.diagram[node]['inflows']
for line in inflows:
source_node = line.source
if source_node not in node_positions:
node_positions[source_node] = node_positions[node] - 1
else:
node_positions[source_node] = min(node_positions[source_node], node_positions[node] - 1)
trace_back(source_node)
def trace_forward(node: Node):
outflows = self.diagram[node]['outflows']
for line in outflows:
target_node = line.target
if target_node not in node_positions:
node_positions[target_node] = node_positions[node] + 1
else:
node_positions[target_node] = max(node_positions[target_node], node_positions[node] + 1)
trace_forward(target_node)
for node in self.diagram:
if node not in node_positions:
node_positions[node] = 0
trace_back(node)
trace_forward(node)这里定义了一个词典 node_position 用来记录节点的水平位置,而后定义了两个递推函数 trace_back 和 trace_forward 分别用来逆流和顺流。最后用一个循环来对所有(经过递推后)还未分配位置的节点来递推地计算它们的水平位置。
最后为了方便起见,对位置进行了平移,来确保节点的位置看起来比较对称(所以虽然说不考虑非联通的情况,但实际上这里处理非联通的图应该也没有太大的问题),并且位置从0开始方便后续排列:
pos = [p for p in node_positions.values()]
mean_pos = sum(pos) / len(pos)
for node in node_positions:
node_positions[node] -= round(mean_pos)
min_pos = min(node_positions.values())
for node in node_positions:
node_positions[node] -= min_pos
return node_positions虽然确实没有有环的情况,但如果真的有怎么办呢?其实也很简单。首先做环路检测把所有环找出来。做环路检测最简单的方式就是从一个节点出发开始沿一个方向遍历,看会不会遇到已经经过的节点。然后按路径长短依次分配每个环的位置,再固定这些位置不动按照上面说的方法安排其他节点的位置即可。不过说起来容易,也有现成的代码可抄(毕竟说白了整张Sankey图就是一堆交织在一起的链表),但毕竟几乎用不上,就不管了。
然后一个问题就是计算节点的流量了。主要的问题在于要保证节点的总流量和进或出节点的线的流量之和严格相等。这一点可以用 Python 的 Decimal 解决。但考虑到在笔者的情况下,各线之间的流量有数量级的差别,因此会很难指定 Decimal 的精度。当然也可以设定取几位小数,但如果这样的话,在笔者这种简单的情景下,不如直接用 int 好了。所以代码就像下面这样。首先把图复制一份,以免直接修改原始数据,后续生成LaTeX代码都用新复制的图:
diagram: dict[Node, NodeInfo] = {}
for node in self.diagram:
diagram[node] = {'inflows': [line.copy() for line in self.diagram[node]['inflows']],
'outflows': [line.copy() for line in self.diagram[node]['outflows']]}而后进行实际的计算:
scale_factor = 1/min_val
for node in diagram:
for line in diagram[node]['inflows']:
line.val = round(line.val * scale_factor)
for line in diagram[node]['outflows']:
line.val = round(line.val * scale_factor)首先选择最小的流量,用这个流量对所有流量进行缩放并四舍五入到整数。
dummy_node = Node("00","00")
node_vals: dict[Node, int] = {}
for node in diagram:
if diagram[node]['inflows']:
inflow_val = sum(line.val for line in diagram[node]['inflows'])
else:
inflow_val = 0
if diagram[node]['outflows']:
outflow_val = sum(line.val for line in diagram[node]['outflows'])
else:
outflow_val = 0
assert isinstance(inflow_val, int) and isinstance(outflow_val, int), "Node values must be integers after scaling and rounding!"
node_val = max(inflow_val, outflow_val)
node_vals[node] = node_val
# add dummy inflow lines or outflow lines if necessary; if no inflow or outflow, no need to add
if inflow_val < node_val and inflow_val > 0:
dummy_line = Line(dummy_node, node, node_val - inflow_val)
diagram[node]['inflows'].append(dummy_line)
if outflow_val < node_val and outflow_val > 0:
dummy_line = Line(node, dummy_node, node_val - outflow_val)
diagram[node]['outflows'].append(dummy_line)然后用 node_vals 这个词典来存储每个节点缩放后的流量。整型相加减不会有精度问题。最后如果一个节点流入和流出的不平衡,就把不平衡的部分指向 dummy_node 并将对应的线添加到图里面。
但是要注意,上面计算的部分应该在生成LaTeX代码前的最后一步进行,以免添加进来的 dummy_node 和相应的线干扰其他计算。
最后是分配颜色的部分。这里为了方便起见,使用两个词典, colormaps 和 node_colors, 前者是从颜色名称到16进制RGB的映射,后者是从节点到颜色名称的映射。同时在代码中加入默认的 colormaps 和当 colormaps 没有给定值时,从 node_colors 中提取16进制RGB并生成 colormaps 的功能:
# process colors
if not colormaps:
if node_colors:
# check if all color strs are legal hex color codes
for node, color_str in node_colors.items():
if not self._is_color_code_legal(color_str):
print(f"Warning: Color string {color_str} for node {node} is not a legal hex color code. Using default colormap instead.")
colormaps = self.default_colormaps
node_colors = {}
break
else:
colors = set(node_colors.values())
for i, color in enumerate(colors):
colormaps[f'UserColor{i}'] = color
else:
colormaps = self.default_colormaps这里强迫症手搓了一个判断16进制RGB字符串是否合法的方法:
def _is_color_code_legal(self, color_str: str) -> bool:
'''
Checks if a given color string is a legal hex color code.
Args:
color_str (str): The color string to check.
Returns:
bool: True if the color string is a legal hex color code, False otherwise.
'''
islegal = True
if not isinstance(color_str, str):
islegal = False
if len(color_str) != 7 or not color_str.startswith('#'):
islegal = False
color_rgb = (color_str[1:3], color_str[3:5], color_str[5:7])
try:
for channel in color_rgb:
if 0 <= int(channel, 16) <= 255:
continue
else:
islegal = False
except ValueError:
islegal = False
return islegal剩下的就是无聊的字符串拼接了,所以略过。那么Google的那个例子,就使用这样的 Python 代码:
import SankeyDiagram as sd
colors = {'cyan': '#a6cee3', 'lime': '#b2df8a', 'red': '#fb9a99', 'orange': '#fdbf6f',
'violet': '#cab2d6', 'yellow': '#ffff99', 'blue': '#1f78b4', 'green': '#33a02c'}
country_colors = {'CA': 'red', 'US': 'orange', 'MX': 'orange', 'BR': 'cyan', 'FR': 'lime', 'GB': 'red', 'SP': 'lime', 'PT': 'cyan', 'ML': 'blue', 'SN': 'violet', 'MA': 'yellow', 'AO': 'violet', 'ZA': 'yellow', 'IN': 'green', 'JP': 'green', 'CN': 'blue'}
countries = [('CA', 'Canada'), ('US', 'United States'), ('MX', 'Mexico'), ('BR', 'Brazil'),
('FR', 'France'), ('GB', 'United Kingdom'), ('SP', 'Spain'), ('PT', 'Portugal'),
('ML', 'Mali'), ('SN', 'Senegal'), ('MA', 'Morocco'), ('AO', 'Angola'),
('ZA', 'South Africa'), ('IN', 'India'), ('JP', 'Japan'), ('CN', 'China')]
ca = sd.Node('CA', 'Canada'); us = sd.Node('US', 'United States'); mx = sd.Node('MX', 'Mexico'); br = sd.Node('BR', 'Brazil'); fr = sd.Node('FR', 'France'); gb = sd.Node('GB', 'United Kingdom'); sp = sd.Node('SP', 'Spain'); pt = sd.Node('PT', 'Portugal'); ml = sd.Node('ML', 'Mali'); sn = sd.Node('SN', 'Senegal'); ma = sd.Node('MA', 'Morocco'); ao = sd.Node('AO', 'Angola'); za = sd.Node('ZA', 'South Africa'); ind = sd.Node('IN', 'India'); jp = sd.Node('JP', 'Japan'); cn = sd.Node('CN', 'China')
sankey = sd.SankeyDiagram()
sankey.add_node(ca); sankey.add_node(us); sankey.add_node(mx); sankey.add_node(br)
sankey.add_node(fr); sankey.add_node(gb); sankey.add_node(sp); sankey.add_node(pt)
sankey.add_node(ml); sankey.add_node(sn); sankey.add_node(ma); sankey.add_node(ao)
sankey.add_node(za); sankey.add_node(ind); sankey.add_node(jp); sankey.add_node(cn)
lines = [(br, pt, 5), (br, fr, 1), (br, sp, 1), (br, gb, 1), (ca, pt, 1), (ca, fr, 5), (ca, gb, 1), (mx, pt, 1), (mx, fr, 1), (mx, sp, 5), (mx, gb, 1), (us, pt, 1), (us, fr, 1), (us, sp, 1), (us, gb, 5), (pt, ao, 2), (pt, sn, 1), (pt, ma, 1), (pt, za, 3), (fr, ao, 1), (fr, sn, 3), (fr, ml, 3), (fr, ma, 3), (fr, za, 1), (sp, sn, 1), (sp, ma, 3), (sp, za, 1), (gb, ao, 1), (gb, sn, 1), (gb, ma, 2), (gb, za, 7), (za, cn, 5), (za, ind, 1), (za, jp, 3), (ao, cn, 5), (ao, ind, 1), (ao, jp, 3), (sn, cn, 5), (sn, ind, 1), (sn, jp, 3), (ml, cn, 5), (ml, ind, 1), (ml, jp, 3), (ma, cn, 5), (ma, ind, 1), (ma, jp, 3)]
for line in lines:
sankey.add_line(source=line[0], target=line[1], val=line[2])
code = sankey.generate_latex_code()
print(code)就会生成这样的LaTeX代码:
\documentclass{standalone}
\usepackage{tikz}
\usepackage{sankey}
\begin{document}
\begin{tikzpicture}
\begin{sankeydiagram}
\sankeyset{ratio=1cm/7,
draw/.style={draw=none,line width=0pt},
color/.style={fill/.style={fill=#1,fill opacity=.75}},
shade/.style 2 args={fill/.style={left color=#1,right color=#2,fill opacity=.5}},
%colors
@define HTML color/.code args={#1/#2}{\definecolor{#1}{HTML}{#2}},
@define HTML color/.list={
blue/1f77b4,orange/ff7f0e,green/2ca02c,red/d62728,purple/9467bd,brown/8c564b,pink/e377c2,gray/7f7f7f,olive/bcbd22,cyan/17becf},
%colors of nodes
@let material color/.code args={#1/#2}{\colorlet{#1}[rgb]{#2}},
@let material color/.list={
CA/blue,US/orange,MX/green,BR/red,FR/blue,GB/orange,SP/green,PT/red,ML/blue,SN/orange,MA/green,AO/red,ZA/purple,IN/blue,JP/orange,CN/green},
}
%lengths
\def\vdist{5mm}
\def\hwidth{.5em}
\def\hdist{8.2cm}
\def\xshift{3em}
\def\separation{.1em}
%nodes
\sankeynode{name=CA,quantity=7}
\sankeynode{name=US,quantity=8,at={[yshift=\vdist]CA.left},anchor=right}
\sankeynode{name=MX,quantity=8,at={[yshift=\vdist]US.left},anchor=right}
\sankeynode{name=BR,quantity=8,at={[yshift=\vdist]MX.left},anchor=right}
\sankeynode{name=FR,quantity=11,at={[xshift=\hdist]CA.right},anchor=right}
\sankeynode{name=GB,quantity=11,at={[yshift=\vdist]FR.left},anchor=right}
\sankeynode{name=SP,quantity=7,at={[yshift=\vdist]GB.left},anchor=right}
\sankeynode{name=PT,quantity=8,at={[yshift=\vdist]SP.left},anchor=right}
\sankeynode{name=ML,quantity=9,at={[xshift=\hdist]FR.right},anchor=right}
\sankeynode{name=SN,quantity=9,at={[yshift=\vdist]ML.left},anchor=right}
\sankeynode{name=MA,quantity=9,at={[yshift=\vdist]SN.left},anchor=right}
\sankeynode{name=AO,quantity=9,at={[yshift=\vdist]MA.left},anchor=right}
\sankeynode{name=ZA,quantity=12,at={[yshift=\vdist]AO.left},anchor=right}
\sankeynode{name=IN,quantity=5,at={[xshift=\hdist]ML.right},anchor=right}
\sankeynode{name=JP,quantity=15,at={[yshift=\vdist]IN.left},anchor=right}
\sankeynode{name=CN,quantity=25,at={[yshift=\vdist]JP.left},anchor=right}
%draw nodes
\sankeyadvance[color=CA]{CA}{\hwidth}
\sankeyadvance[color=US]{US}{\hwidth}
\sankeyadvance[color=MX]{MX}{\hwidth}
\sankeyadvance[color=BR]{BR}{\hwidth}
\sankeyadvance[color=FR]{FR}{\hwidth}
\sankeyadvance[color=GB]{GB}{\hwidth}
\sankeyadvance[color=SP]{SP}{\hwidth}
\sankeyadvance[color=PT]{PT}{\hwidth}
\sankeyadvance[color=ML]{ML}{\hwidth}
\sankeyadvance[color=SN]{SN}{\hwidth}
\sankeyadvance[color=MA]{MA}{\hwidth}
\sankeyadvance[color=AO]{AO}{\hwidth}
\sankeyadvance[color=ZA]{ZA}{\hwidth}
\sankeyadvance[color=IN]{IN}{\hwidth}
\sankeyadvance[color=JP]{JP}{\hwidth}
\sankeyadvance[color=CN]{CN}{\hwidth}
\sankeyfork{CA}{1/CA-to-PT,1/CA-to-GB,5/CA-to-FR}
\sankeyfork{US}{1/US-to-PT,1/US-to-SP,5/US-to-GB,1/US-to-FR}
\sankeyfork{MX}{1/MX-to-PT,5/MX-to-SP,1/MX-to-GB,1/MX-to-FR}
\sankeyfork{BR}{5/BR-to-PT,1/BR-to-SP,1/BR-to-GB,1/BR-to-FR}
\sankeyfork{FR}{1/FR-from-BR,1/FR-from-MX,1/FR-from-US,5/FR-from-CA,3/FR-from-00}
\sankeyfork{FR}{1/FR-to-ZA,1/FR-to-AO,3/FR-to-MA,3/FR-to-SN,3/FR-to-ML}
\sankeyfork{GB}{1/GB-from-BR,1/GB-from-MX,5/GB-from-US,1/GB-from-CA,3/GB-from-00}
\sankeyfork{GB}{7/GB-to-ZA,1/GB-to-AO,2/GB-to-MA,1/GB-to-SN}
\sankeyfork{SP}{1/SP-from-BR,5/SP-from-MX,1/SP-from-US}
\sankeyfork{SP}{1/SP-to-ZA,3/SP-to-MA,1/SP-to-SN,2/SP-to-00}
\sankeyfork{PT}{5/PT-from-BR,1/PT-from-MX,1/PT-from-US,1/PT-from-CA}
\sankeyfork{PT}{3/PT-to-ZA,2/PT-to-AO,1/PT-to-MA,1/PT-to-SN,1/PT-to-00}
\sankeyfork{ML}{3/ML-from-FR,6/ML-from-00}
\sankeyfork{ML}{5/ML-to-CN,3/ML-to-JP,1/ML-to-IN}
\sankeyfork{SN}{1/SN-from-PT,1/SN-from-SP,1/SN-from-GB,3/SN-from-FR,3/SN-from-00}
\sankeyfork{SN}{5/SN-to-CN,3/SN-to-JP,1/SN-to-IN}
\sankeyfork{MA}{1/MA-from-PT,3/MA-from-SP,2/MA-from-GB,3/MA-from-FR}
\sankeyfork{MA}{5/MA-to-CN,3/MA-to-JP,1/MA-to-IN}
\sankeyfork{AO}{2/AO-from-PT,1/AO-from-GB,1/AO-from-FR,5/AO-from-00}
\sankeyfork{AO}{5/AO-to-CN,3/AO-to-JP,1/AO-to-IN}
\sankeyfork{ZA}{3/ZA-from-PT,1/ZA-from-SP,7/ZA-from-GB,1/ZA-from-FR}
\sankeyfork{ZA}{5/ZA-to-CN,3/ZA-to-JP,1/ZA-to-IN,3/ZA-to-00}
\sankeyfork{IN}{1/IN-from-ZA,1/IN-from-AO,1/IN-from-MA,1/IN-from-SN,1/IN-from-ML}
\sankeyfork{JP}{3/JP-from-ZA,3/JP-from-AO,3/JP-from-MA,3/JP-from-SN,3/JP-from-ML}
\sankeyfork{CN}{5/CN-from-ZA,5/CN-from-AO,5/CN-from-MA,5/CN-from-SN,5/CN-from-ML}
%link nodes
\sankeyoutin[shade={BR}{FR}]{BR-to-FR}{FR-from-BR}
\sankeyoutin[shade={MX}{FR}]{MX-to-FR}{FR-from-MX}
\sankeyoutin[shade={US}{FR}]{US-to-FR}{FR-from-US}
\sankeyoutin[shade={CA}{FR}]{CA-to-FR}{FR-from-CA}
\sankeyoutin[shade={BR}{GB}]{BR-to-GB}{GB-from-BR}
\sankeyoutin[shade={MX}{GB}]{MX-to-GB}{GB-from-MX}
\sankeyoutin[shade={US}{GB}]{US-to-GB}{GB-from-US}
\sankeyoutin[shade={CA}{GB}]{CA-to-GB}{GB-from-CA}
\sankeyoutin[shade={BR}{SP}]{BR-to-SP}{SP-from-BR}
\sankeyoutin[shade={MX}{SP}]{MX-to-SP}{SP-from-MX}
\sankeyoutin[shade={US}{SP}]{US-to-SP}{SP-from-US}
\sankeyoutin[shade={BR}{PT}]{BR-to-PT}{PT-from-BR}
\sankeyoutin[shade={MX}{PT}]{MX-to-PT}{PT-from-MX}
\sankeyoutin[shade={US}{PT}]{US-to-PT}{PT-from-US}
\sankeyoutin[shade={CA}{PT}]{CA-to-PT}{PT-from-CA}
\sankeyoutin[shade={FR}{ML}]{FR-to-ML}{ML-from-FR}
\sankeyoutin[shade={PT}{SN}]{PT-to-SN}{SN-from-PT}
\sankeyoutin[shade={SP}{SN}]{SP-to-SN}{SN-from-SP}
\sankeyoutin[shade={GB}{SN}]{GB-to-SN}{SN-from-GB}
\sankeyoutin[shade={FR}{SN}]{FR-to-SN}{SN-from-FR}
\sankeyoutin[shade={PT}{MA}]{PT-to-MA}{MA-from-PT}
\sankeyoutin[shade={SP}{MA}]{SP-to-MA}{MA-from-SP}
\sankeyoutin[shade={GB}{MA}]{GB-to-MA}{MA-from-GB}
\sankeyoutin[shade={FR}{MA}]{FR-to-MA}{MA-from-FR}
\sankeyoutin[shade={PT}{AO}]{PT-to-AO}{AO-from-PT}
\sankeyoutin[shade={GB}{AO}]{GB-to-AO}{AO-from-GB}
\sankeyoutin[shade={FR}{AO}]{FR-to-AO}{AO-from-FR}
\sankeyoutin[shade={PT}{ZA}]{PT-to-ZA}{ZA-from-PT}
\sankeyoutin[shade={SP}{ZA}]{SP-to-ZA}{ZA-from-SP}
\sankeyoutin[shade={GB}{ZA}]{GB-to-ZA}{ZA-from-GB}
\sankeyoutin[shade={FR}{ZA}]{FR-to-ZA}{ZA-from-FR}
\sankeyoutin[shade={ZA}{IN}]{ZA-to-IN}{IN-from-ZA}
\sankeyoutin[shade={AO}{IN}]{AO-to-IN}{IN-from-AO}
\sankeyoutin[shade={MA}{IN}]{MA-to-IN}{IN-from-MA}
\sankeyoutin[shade={SN}{IN}]{SN-to-IN}{IN-from-SN}
\sankeyoutin[shade={ML}{IN}]{ML-to-IN}{IN-from-ML}
\sankeyoutin[shade={ZA}{JP}]{ZA-to-JP}{JP-from-ZA}
\sankeyoutin[shade={AO}{JP}]{AO-to-JP}{JP-from-AO}
\sankeyoutin[shade={MA}{JP}]{MA-to-JP}{JP-from-MA}
\sankeyoutin[shade={SN}{JP}]{SN-to-JP}{JP-from-SN}
\sankeyoutin[shade={ML}{JP}]{ML-to-JP}{JP-from-ML}
\sankeyoutin[shade={ZA}{CN}]{ZA-to-CN}{CN-from-ZA}
\sankeyoutin[shade={AO}{CN}]{AO-to-CN}{CN-from-AO}
\sankeyoutin[shade={MA}{CN}]{MA-to-CN}{CN-from-MA}
\sankeyoutin[shade={SN}{CN}]{SN-to-CN}{CN-from-SN}
\sankeyoutin[shade={ML}{CN}]{ML-to-CN}{CN-from-ML}
%labels
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]CA) {Canada};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]US) {United States};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]MX) {Mexico};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]BR) {Brazil};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]FR) {France};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]GB) {United Kingdom};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]SP) {Spain};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=-\xshift]PT) {Portugal};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]ML) {Mali};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]SN) {Senegal};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]MA) {Morocco};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]AO) {Angola};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]ZA) {South Africa};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]IN) {India};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]JP) {Japan};
\node[anchor=base,inner sep=\separation,align=center,font=\small] at ([xshift=\xshift]CN) {China};
\end{sankeydiagram}
\end{tikzpicture}
\end{document}
这里笔者偷懒就没有使用 \foreach 来节约行数了。虽然要改一下应该也很简单就是了。另外为了节约键盘,这里使用了copliot帮忙转换一下代码格式,不过好像copilot对于着色有自己的想法,总之就导致了这样的图:
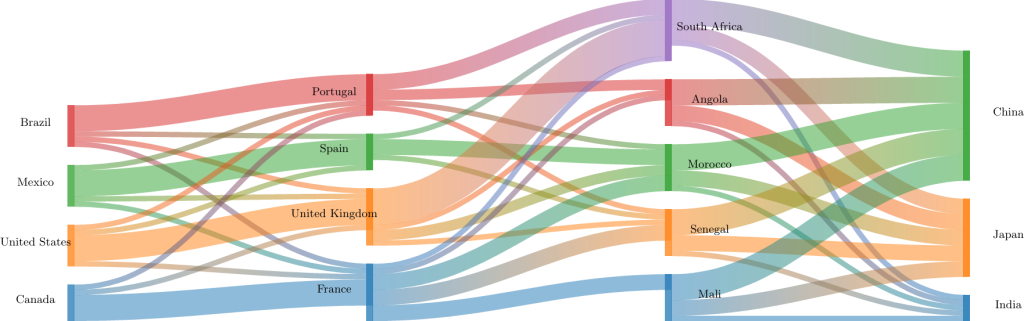
看起来还不错,作为一个模板已经很像样了。
附录
最后附上代码。算上注释和一些文档,整套代码421行,如下所示:
from typing import Optional, TypedDict, Literal
class Node:
'''
Represents a node in the Sankey diagram.
The node can be identified by a unique name and an optional label.
The quantity associated with the node is determined by the sum of incoming and outgoing lines and will be caculated when generates the diagram, thus not included in this class.
Attributes:
name (str): The unique identifier for the node. "00" is reserved for dummy nodes.
label (str): The display label for the node. If not provided, it defaults to the name. "00" is reserved for dummy nodes.
Latex codes is of course supported in the label.
'''
def __init__(self, name: str, label: str = ""):
self.name = name
self.label = label if label else name
def __repr__(self) -> str:
return f"Sankey node(name={self.name}, label={self.label})"
def __eq__(self, other: object) -> bool:
if not isinstance(other, Node):
return NotImplemented
return self.name == other.name and self.label == other.label
def __hash__(self) -> int:
return hash((self.name, self.label))
def copy(self) -> 'Node':
return Node(self.name, self.label)
class Line:
'''
Represents a directed line connecting two nodes in the Sankey diagram.
Attributes:
source (Node): The starting node of the line.
target (Node): The ending node of the line.
val (float | int): The flux of the line.
'''
def __init__(self, source: Node, target: Node, val: float | int):
self.source = source
self.target = target
if val <= 0:
raise ValueError("The value of a Sankey line must be positive.")
self.val = val
def __repr__(self) -> str:
return f"Sankey line ({self.source} -> {self.target} : {self.val})"
def __eq__(self, other: object) -> bool:
if not isinstance(other, Line):
return NotImplemented
return self.source == other.source and self.target == other.target and self.val == other.val
def __hash__(self) -> int:
return hash((self.source, self.target, self.val))
def copy(self) -> 'Line':
return Line(self.source.copy(), self.target.copy(), self.val)
def latex_repr(self, direction: Literal['to', 'from']) -> str:
if direction == 'to':
return f"{self.val}/{self.source.name}-{direction}-{self.target.name}"
elif direction == 'from':
return f"{self.val}/{self.target.name}-{direction}-{self.source.name}"
else:
raise ValueError("Direction must be either 'to' or 'from'.")
class NodeInfo(TypedDict):
inflows: list[Line]
outflows: list[Line]
class SankeyDiagram:
'''
Represents a Sankey diagram consisting of nodes and directed lines.
Attributes:
nodes (list[Node]): A list of nodes in the diagram.
When generating the diagram, the quantity of each node will be calculated based on the connected lines.
The node with smaller index in the list will be placed on the bottom.
lines (list[Line]): A list of directed lines connecting the nodes.
'''
default_colormaps = {
'blue': '#1f77b4',
'orange': '#ff7f0e',
'green': '#2ca02c',
'red': '#d62728',
'purple': '#9467bd',
'brown': '#8c564b',
'pink': '#e377c2',
'gray': '#7f7f7f',
'olive': '#bcbd22',
'cyan': '#17becf'
}
@property
def diagram(self):
if not self._diagram:
self._generate_diagram()
return self._diagram
def __init__(self):
self.nodes: list[Node] = []
self.lines: list[Line] = []
self._diagram: dict[Node, NodeInfo] = {}
def add_node(self, node: Optional[Node] = None, name: str = "", label: str = "") -> Node:
if not node and (not name or not label):
raise ValueError("Either a Node object or both name and label must be provided to add a new node.")
if not node:
node = Node(name, label)
if node in self.nodes:
print(f"Warning: Node {node} already exists in the diagram and thus will not be added.")
return node
self.nodes.append(node)
return node
def add_line(self, line: Optional[Line] = None, source: Optional[Node] = None, target: Optional[Node] = None, val: Optional[float] = None) -> Line:
if line is None:
if source is None or target is None or val is None:
raise ValueError("Either a Line object or source, target, and val must be provided to add a new line.")
line = Line(source, target, val)
if line in self.lines:
print(f"Warning: Line {line} already exists in the diagram and thus will not be added.")
else:
self.lines.append(line)
# auto add nodes if they do not exist
if line.source not in self.nodes:
self.add_node(node=line.source)
if line.target not in self.nodes:
self.add_node(node=line.target)
return line
def _generate_diagram(self):
for node in self.nodes:
self._diagram[node] = {'inflows': [], 'outflows': []}
for line in self.lines:
self._diagram[line.source]['outflows'].append(line)
self._diagram[line.target]['inflows'].append(line)
# check for isolated nodes
for node in self.nodes:
if not self._diagram[node]['inflows'] and not self._diagram[node]['outflows']:
print(f"Warning: Node {node} is isolated and has no inflows or outflows.")
self._diagram.pop(node)
# rearrange the lines based on the reversed node order
reversed_nodes = self.nodes[::-1]
for node in reversed_nodes:
inflows = self._diagram[node]['inflows']
outflows = self._diagram[node]['outflows']
inflows.sort(key=lambda line: reversed_nodes.index(line.source))
outflows.sort(key=lambda line: reversed_nodes.index(line.target))
self._diagram[node]['inflows'] = inflows
self._diagram[node]['outflows'] = outflows
def determine_node_x_positions(self) -> dict[Node, int]:
'''
Determines the x-axis positions of nodes in the Sankey diagram based on their connections.
Returns:
dict[Node, int]: A dictionary mapping each node to its x-axis position.
'''
node_positions: dict[Node, int] = {}
def trace_back(node: Node):
inflows = self.diagram[node]['inflows']
for line in inflows:
source_node = line.source
if source_node not in node_positions:
node_positions[source_node] = node_positions[node] - 1
else:
node_positions[source_node] = min(node_positions[source_node], node_positions[node] - 1)
trace_back(source_node)
def trace_forward(node: Node):
outflows = self.diagram[node]['outflows']
for line in outflows:
target_node = line.target
if target_node not in node_positions:
node_positions[target_node] = node_positions[node] + 1
else:
node_positions[target_node] = max(node_positions[target_node], node_positions[node] + 1)
trace_forward(target_node)
for node in self.diagram:
if node not in node_positions:
node_positions[node] = 0
trace_back(node)
trace_forward(node)
# balance the positions and then start from 0
pos = [p for p in node_positions.values()]
mean_pos = sum(pos) / len(pos)
for node in node_positions:
node_positions[node] -= round(mean_pos)
min_pos = min(node_positions.values())
for node in node_positions:
node_positions[node] -= min_pos
return node_positions
def _is_color_code_legal(self, color_str: str) -> bool:
'''
Checks if a given color string is a legal hex color code.
Args:
color_str (str): The color string to check.
Returns:
bool: True if the color string is a legal hex color code, False otherwise.
'''
islegal = True
if not isinstance(color_str, str):
islegal = False
if len(color_str) != 7 or not color_str.startswith('#'):
islegal = False
color_rgb = (color_str[1:3], color_str[3:5], color_str[5:7])
try:
for channel in color_rgb:
if 0 <= int(channel, 16) <= 255:
continue
else:
islegal = False
except ValueError:
islegal = False
return islegal
def generate_latex_code(self, ratio: str = "", colormaps: dict[str, str] = {}, node_colors: dict[Node, str] = {}, compilable: bool = True) -> str:
'''
Generates LaTeX code for the Sankey diagram using the sankey package.
Args:
ratio (str): The ratio setting for the sankey diagram in LaTeX.
This controls the scaling of the diagram.
Use a string like "1cm/10" to set the ratio, the former part is the length (width) representing the latter part value of the flow,
i. e. 1cm length represents 10 units of flow.
If not provided, 1cm will represent the largest flow value.
colormaps (dict[str, str]): A dictionary mapping colormap names to hex color codes (i. e. "#9999FF").
If not provided, all the strings in node_colors must be hex color codes, or a default colormap will be used.
node_colors (dict[Node, str]): A dictionary mapping nodes to specific color names defined in colormaps.
If not provided, nodes will be colored based on the order of appearance using the colormaps.
compilable (bool): If True, the generated LaTeX code will include the document class and package imports, making it directly compilable.
If False, document class and package imports will be cited out, suitable for inclusion in a larger LaTeX document. Default is True.
Returns:
str: The LaTeX code representing the Sankey diagram.
'''
# In sankey package the quantity of each node must strictly equal to the sum of inflows and outflows.
# Thus first we need to scale the values to fit in this range according to the maximum and the given precision.
# get a copy of the diagram to avoid modifying the original values
diagram: dict[Node, NodeInfo] = {}
for node in self.diagram:
diagram[node] = {'inflows': [line.copy() for line in self.diagram[node]['inflows']],
'outflows': [line.copy() for line in self.diagram[node]['outflows']]}
min_val = min(line.val for line in self.lines)
# round and transfer all values to int for precision control
scale_factor = 1/min_val
for node in diagram:
for line in diagram[node]['inflows']:
line.val = round(line.val * scale_factor)
for line in diagram[node]['outflows']:
line.val = round(line.val * scale_factor)
# generate list of lines for convenience; note that each line appears twice in the diagram dict
all_lines = [line for node in diagram for line in diagram[node]['inflows']]
# get the nodes at each position
position_nodes: dict[int, list[Node]] = {}
node_positions = self.determine_node_x_positions()
for node, pos in node_positions.items():
if pos not in position_nodes:
position_nodes[pos] = []
position_nodes[pos].append(node)
# order the nodes at each position based on their order in self.nodes
for pos in position_nodes:
position_nodes[pos].sort(key=lambda node: self.nodes.index(node))
# process colors
if not colormaps:
if node_colors:
# check if all color strs are legal hex color codes
for node, color_str in node_colors.items():
if not self._is_color_code_legal(color_str):
print(f"Warning: Color string {color_str} for node {node} is not a legal hex color code. Using default colormap instead.")
colormaps = self.default_colormaps
node_colors = {}
break
else:
colors = set(node_colors.values())
for i, color in enumerate(colors):
colormaps[f'UserColor{i}'] = color
else:
colormaps = self.default_colormaps
if not node_colors:
# assign colors based on the order of appearance
color_names = list(colormaps.keys())
for nodes in position_nodes.values():
for i, node in enumerate(nodes):
color_name = color_names[i % len(color_names)]
node_colors[node] = color_name
# finally caculates the node values and balance the inflows and outflows to avoid errors from dummy nodes/lines;
# nodes value is the maxium between inflows and outflows;
# add dummy lines and nodes if necessary
dummy_node = Node("00","00")
node_vals: dict[Node, int] = {}
for node in diagram:
if diagram[node]['inflows']:
inflow_val = sum(line.val for line in diagram[node]['inflows'])
else:
inflow_val = 0
if diagram[node]['outflows']:
outflow_val = sum(line.val for line in diagram[node]['outflows'])
else:
outflow_val = 0
assert isinstance(inflow_val, int) and isinstance(outflow_val, int), "Node values must be integers after scaling and rounding!"
node_val = max(inflow_val, outflow_val)
node_vals[node] = node_val
# add dummy inflow lines or outflow lines if necessary; if no inflow or outflow, no need to add
if inflow_val < node_val and inflow_val > 0:
dummy_line = Line(dummy_node, node, node_val - inflow_val)
diagram[node]['inflows'].append(dummy_line)
if outflow_val < node_val and outflow_val > 0:
dummy_line = Line(node, dummy_node, node_val - outflow_val)
diagram[node]['outflows'].append(dummy_line)
################ generate LaTeX code ################
# preamble and many begins
begin = [r"\documentclass{standalone}"+"\n",
r"\usepackage{tikz}"+"\n",
r"\usepackage{sankey}"+"\n",
r"\begin{document}"+"\n",
]
if compilable:
latex_code = "".join(begin)
else:
begin = [r"%"+line for line in begin]
latex_code = "".join(begin)
latex_code += r"\begin{tikzpicture}" + "\n"
latex_code += r"\begin{sankeydiagram}" + "\n"
# sankey setting
settings = r"\sankeyset{"
if not ratio:
max_val = max(line.val for line in all_lines)
ratio = "1cm/" + str(max_val)
settings += f"ratio={ratio},\n"
settings += r"draw/.style={draw=none,line width=0pt},"+"\n"
settings += r"color/.style={fill/.style={fill=#1,fill opacity=.75}},"+"\n"
settings += r"shade/.style 2 args={fill/.style={left color=#1,right color=#2,fill opacity=.5}},"+"\n"
# define colors
settings += r"%colors"+ "\n"
settings += r"@define HTML color/.code args={#1/#2}{\definecolor{#1}{HTML}{#2}},"+"\n"
settings += r"@define HTML color/.list={"+"\n"
for color_name, color_code in colormaps.items():
# remove the leading '#' and lowercase the letters
color_code = color_code.lstrip('#').lower()
settings += f"{color_name}/{color_code},"
settings = settings.rstrip(',') + r"}," + "\n"
settings += r"%colors of nodes" + "\n"
settings += r"@let material color/.code args={#1/#2}{\colorlet{#1}[rgb]{#2}}," + "\n"
settings += r"@let material color/.list={" + "\n"
for node, color_name in node_colors.items():
settings += f"{node.name}/{color_name},"
settings = settings.rstrip(',') + r"}," + "\n"
settings += r"}" + "\n"
latex_code += settings
# define lengths
latex_code += r"%lengths" + "\n"
latex_code += r"\def\vdist{5mm}" + "\n" # vertical distance between nodes
latex_code += r"\def\hwidth{.5em}" + "\n" # node width (not representing any value but only for aesthetics! Nodes value is represented by the height of the node!)
latex_code += r"\def\hdist{8.2cm}" + "\n" # horizontal distance between nodes
latex_code += r"\def\xshift{3em}" + "\n" # x shift between nodes and labels
latex_code += r"\def\separation{.1em}" + "\n" # separation between label and tikz node of the label (the 'inner sep' key in tikz)
# add nodes
latex_code += r"%nodes" + "\n"
for pos in sorted(position_nodes.keys()):
nodes = position_nodes[pos]
for i, node in enumerate(nodes):
if pos == 0 and i == 0: # no need to specify position for the first node
latex_code += r"\sankeynode{"+f"name={node.name},quantity={node_vals[node]}"+r"}"+ "\n"
else:
if i == 0:
latex_code +=\
r"\sankeynode{"+f"name={node.name},quantity={node_vals[node]}"+r",at={[xshift=\hdist]"+f"{position_nodes[pos-1][0].name}.right"+r"},anchor=right}"+ "\n"
else:
latex_code +=\
r"\sankeynode{"+f"name={node.name},quantity={node_vals[node]}"+r",at={[yshift=\vdist]"+f"{nodes[i-1].name}.left"+r"},anchor=right}"+ "\n"
# draw nodes and fork them
latex_code += r"%draw nodes" + "\n"
for node in diagram:
latex_code += r"\sankeyadvance[color=" + node.name + r"]{" + node.name + r"}{" + r"\hwidth" + "}\n"
# the two for loop is not combined only because aesthetics of the generated code
for node in diagram:
lines = diagram[node]['inflows']
if len(lines) > 0:
latex_code += r"\sankeyfork{"+f"{node.name}"+r"}{"
# order lines based on the sequence of target nodes in self.nodes
lines.sort(key=lambda line: self.nodes.index(line.target), reverse=True)
for line in lines:
latex_code += line.latex_repr(direction='from') + ","
latex_code = latex_code.rstrip(',') + r"}" + "\n"
lines = diagram[node]['outflows']
if len(lines) > 0:
latex_code += r"\sankeyfork{"+f"{node.name}"+r"}{"
# order lines based on the sequence of source nodes in self.nodes
lines.sort(key=lambda line: self.nodes.index(line.source), reverse=True)
for line in lines:
latex_code += line.latex_repr(direction='to') + ","
latex_code = latex_code.rstrip(',') + r"}" + "\n"
# link nodes
latex_code += r"%link nodes" + "\n"
for line in all_lines:
latex_code += r"\sankeyoutin[shade={" + line.source.name + r"}{" + line.target.name + r"}]" + \
r"{" + line.latex_repr(direction='to').split("/", maxsplit=1)[1] + r"}" + \
r"{" + line.latex_repr(direction='from').split("/", maxsplit=1)[1] + r"}" + "\n"
# labels
latex_code += r"%labels" + "\n"
mean_pos = sum(node_positions.values()) / len(node_positions)
for node in diagram:
pos = node_positions[node]
if pos - mean_pos < 0:
loc = r"[xshift=-\xshift]"
else:
loc = r"[xshift=\xshift]"
latex_code += r"\node[anchor=base,inner sep=\separation,align=center,font=\small] at ("+loc+node.name+") {"+node.label+r"};" + "\n"
# many ends and end document
latex_code += r"\end{sankeydiagram}" + "\n"
latex_code += r"\end{tikzpicture}"+"\n"
ends = [r"\end{document}"+"\n"]
if compilable:
latex_code += "".join(ends)
else:
ends = [r"%"+line for line in ends]
latex_code += "".join(ends)
return latex_code





Comments NOTHING