最近做电磁辐射方面的论文,碰到一个矢量球谐函数展开的方法,很有意思,故作文以记,备不时之需。
一、标量球谐函数(Scalar Spherical Harmonics, SSH)
首先复习SSH的相关知识。SSH是球坐标形式下拉普拉斯方程![]() 角向部分的分离变量解。拉普拉斯方程角向部分分离变量为:
角向部分的分离变量解。拉普拉斯方程角向部分分离变量为:
(1) ![]()
其本征函数为球谐函数![]() ,复数形式为:
,复数形式为:
(2) ![]()
其中,![]() 是连带勒让德多项式:
是连带勒让德多项式:
(3) ![]()
SSH是一组正交完备基:
(4) ![]()
可以将球面上的函数用SSH展开:
(5) 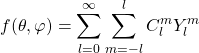
其中,
(6) ![]()
球谐函数具有确定的宇称。可以证明,在宇称算符![]() 作用下,
作用下,![]() :
:
(7) ![]()
根据勒让德多项式的微分表示:
(8) ![]()
容易看出![]() ,故:
,故:
(9) ![]()
因此![]() 。
。
二、矢量球谐函数(Vector Spherical Harmonics, VSH)
为方便起见,本节将尽量使用抽象指标记号。一般的,矢量球谐函数是拉普拉斯方程![]() 角向部分的解。鉴于该方程可以写为分量形式:
角向部分的解。鉴于该方程可以写为分量形式:![]() ,因此根据第一节的内容,很容易看出其各分量在角向的本征函数仍为
,因此根据第一节的内容,很容易看出其各分量在角向的本征函数仍为![]() ,即拉普拉斯方程的解可以写作如下形式:
,即拉普拉斯方程的解可以写作如下形式:
(10) 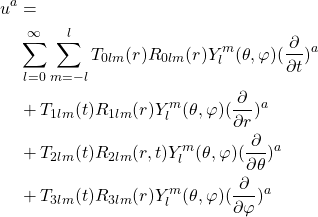
但是,使用这种形式的VSH并没有太大的意义:一方面,考虑如下的矢量方程![]() ,如果分别用VSH和SSH展开
,如果分别用VSH和SSH展开![]() 和
和![]() ,再代入方程,我们容易发现并不能消去
,再代入方程,我们容易发现并不能消去![]() ,从而解出展开系数和
,从而解出展开系数和![]() 之间的关系——而这往往是在求解边值问题时的常规步骤;另一方面,当涉及到旋度时,这样的表示方式往往会遇到困难。因此,我们需要重新引入两个函数:
之间的关系——而这往往是在求解边值问题时的常规步骤;另一方面,当涉及到旋度时,这样的表示方式往往会遇到困难。因此,我们需要重新引入两个函数:![]() 和
和![]() 作为对
作为对![]() 的补充,共同组成VSH。具体的说,就是将
的补充,共同组成VSH。具体的说,就是将![]() 的第
的第![]() 项(
项(![]() )表示为:
)表示为:
(11) ![]()
更进一步的,矢量![]() 可以写为:
可以写为:
(12) 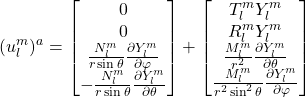
因此,VSH可以看作由以下4类矢量组成:
(13) 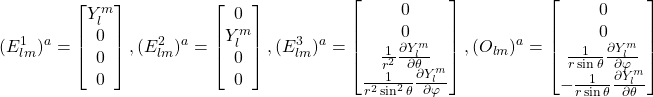
实践中,更常用到的是其对偶矢量:
(14) 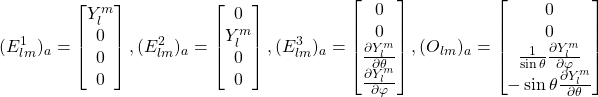
各式中的![]() 已吸收入展开系数中。注意到,前三组矢量宇称为
已吸收入展开系数中。注意到,前三组矢量宇称为![]() ,最后一组矢量宇称为
,最后一组矢量宇称为![]() 。为看到这一点,以最后一组函数为例,由于
。为看到这一点,以最后一组函数为例,由于
(15) ![]()
(16) ![]()
再考虑到![]() ,
,![]() ,因此
,因此![]() ,
,![]() 。故
。故![]() 。同理可得出其他VSH的宇称。
。同理可得出其他VSH的宇称。
VSH是正交完备的。其正交关系不便用抽象指标表出,此处改用一般表示方法。假定![]() 已归一化,
已归一化,![]() 和
和![]() 的正交完备性关系容易看出;对于剩下的两组矢量,则有:
的正交完备性关系容易看出;对于剩下的两组矢量,则有:
(17) ![]()
(18) ![]()
(19) ![]()
任意一个矢量场可以用VSH展开,例如(11)式中,
(20) ![]()
以上各式中![]() 均为单位球面。
均为单位球面。





Comments NOTHING