书接上文，请问，拉格朗日力学中，最激动人心的是什么？当然是自由质点的拉格朗日函数和各守恒量的导出（当然关于这个问题不同的人有不同的看法，但这是我写的文章，所以就采用我的看法x）。为什么这么说呢，因为从下面的推导可以看出来，自由质点（更进一步，封闭系统）的拉格朗日函数和守恒量，“似乎”完全取决于空间的几何。在这一篇中，我们先讲拉格朗日函数的得到；守恒量的推出则放到下一篇中。

一. 惯性参考系，伽利略相对性原理

在经典力学中，有一条重要的假设（用数学的话讲，公设），即“总是存在这样一个参考系，使得空间是均匀而各向同性的，时间也是均匀的”。这样的参考系，称为惯性参考系。什么叫做空间的均匀和各向同性？这里的“空间”包括什么？我们先暂时跳出经典力学的欧氏几何框架来看一看。从直观上来看，所谓“均匀”，无非就是处处都一样。譬如说，一个欧氏空间中的每个点都是等价的，一个球面上的点也都是等价的，但椭球面上的一个点却不一定和另一个点等价——考虑位于椭球面与长轴相交的一个点和与短轴相交的一个点就很容易知道了。我们看到，所谓的“均匀”，实则是一类“平移对称性”。类似的，各向同性也可以解释为“旋转对称性”。为什么这里的“平移对称性”和“旋转对称性”要打引号？因为到目前为止，我们还没有对“平移”和“旋转”做一个解释，更没有说什么叫做“对称性”。由于经典理论力学的背景时空为绝对时空观下的欧氏空间，因此平移和旋转的概念和通常人们脑海中的观念一致；而“对称”则可理解为在变换前后是完全相同的。因此，我们可以从以上讨论中抽象出更数学、更精确的概念：

所谓的“均匀”、“各向同性”的描述，实则是对时空流形（在经典理论力学下即欧氏空间）对称性的反映，即这一时空流形具有哪些单参等度规群。而我们知道，一个单参等度规群对应一个killing矢量场。我们称一个时空是均匀的，当它在某一坐标系下所有的坐标基矢都是killing矢量场；我们称一个时空是各项同性的，如果在极坐标系（球坐标系）下沿角向的坐标基矢场是killing矢量场。

好，相信没有碰过微分几何的读者看到上面这段时一定觉得“这逼在讲啥啊”，不用着急，这就做一点解释（当然详细的说明还是去看微分几何的书比较靠谱，这里只是抛块砖头，上面的定义也不甚严谨）。首先来看“单参等度规群”，它实际上是由两个定语“单参”和“等度规（映射）”修饰的一个名词“群”。“群”应当都有所耳闻了，它的定义也不再复述。一类变换可以用一个群来描述，譬如一个三维的旋转变换就可以用一个旋转群SO3表示。“单参”是指群里的元素可以用一个参数来表征，比如二维旋转变换可以用旋转角度来表征，因此二维旋转变换群是一个单参的群。而“等度规”是一个绝妙的定语，它指出在这个群的群元作用下前后流形不仅是微分同胚，而且是等度规的。等度规意味着什么呢？意味着在变换前后，对应点的度规是相同的。用物理一点的话说，度规在变换作用下不变。而我们知道，一个流形，在物理的全部的深意都藏于它的度规中，因此我们知道，等度规的变换就是我们所说的对称性。因此，我敢于下这样的断言：物理中的对称性即是等度规变换，所有连续对称性都对应一个单参等度规群。

以上几段没看懂也没关系，总之就是理清均匀和各向同性到底在数学上是什么意思，而在物理中，绝大多数情况下都不需要这么咬文嚼字，只需要“我觉得应该是这样”就行了。而关于第二个问题，“空间到底包括什么？”答案也呼之欲出了：经典力学中所说的空间，实则就是一个物质相互作用的背景舞台，不和物质之间互动，也不参与物质之间的作用。这实际上也是绝对时空观的体现。

显然，允许存在的惯性参考系不止一个。例如，假设存在惯性系K，那么将其做平移变换或旋转变换后得到的新参考系K'显然也是惯性系。实验和信念告诉我们，这些惯性系之间应当是平权的，即：

伽利略相对性原理：在不同惯性参考系之中，时间、空间的均匀性相同，力学规律也相同，不同的惯性参考系之间在力学上完全等价。

但不同的惯性参考系依然可能存在区别。我们知道，参考系本质上是一组满足特定条件的特殊观者，因此相对于某参考系K，可以谈及另一参考系K'的运动情况——只需要描述K'中某特定观者的运动情况就行了。若K是惯性系，那做匀速运动的另一参考系K'是否依然是惯性系呢？微分几何的方法告诉我们答案是肯定的，不过过程涉及得太远（其实也不太远）就不详细说明了（当然实验也告诉我们答案是肯定的）。

既然谈到的匀速运动，那就再顺带提一句惯性系中一个极其重要的定律：惯性定律，或称牛顿第一定律，即惯性系中自由质点的运动状态保持不变。这是空间均匀性和各向同性的直接结论。首先，因为空间是均匀的，因此自由质点的拉格朗日函数不应与\boldsymbol{r}有关。具体的说，自由质点的运动亦可以看作对空间进行的一次平移变换，但空间并不因平移变换而变化，即与\boldsymbol{r}无关。于是，结合拉格朗日方程，我们有：

(1)   \begin{equation*} \frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\boldsymbol{r}}}=0 \end{equation*}

因此\partial L/\partial \boldsymbol{v}是一个常矢量。另一方面，空间具有各向同性，因此粒子的运动状态不由运动的方向影响，故而L只能是v^2的函数，即L=L(v^2)。故而\partial L/\partial \boldsymbol{v}=2\boldsymbol{v}L'(v^2)。L'(v^2)显然不能为0，否则所有自由运动质点都具有相同的拉格朗日函数，亦即做相同的运动，而这是不可能的。因此，只能\boldsymbol{v}是一个常矢量，即粒子的速度保持不变。这就是惯性定律。

二. 自由质点与封闭系统的拉格朗日函数

欧氏空间的性质是如此之好，我们甚至能进一步猜出拉格朗日函数的具体形式。不过在这之前，我们需要先停留一下，研究一下拉格朗日函数的一条重要性质。

注意到作用量S和拉格朗日函数L之间的关系为：

(2)   \begin{equation*} S=\int^{t_1}_{t_2}L(q,\,\dot{q},\,t)\mathrm{d}t \end{equation*}

因此如果两个拉格朗日函数之间相差一个坐标与时间的函数对时间的全导数：

(3)   \begin{equation*} L(q,\,\dot{q},\,t)=L'(q,\,t)+\frac{\mathrm{d}}{\mathrm{d}t}f(q,\,t) \end{equation*}

那么就有（注意q(t)也是t的函数）

(4)   \begin{equation*} S=S'+f(q_2,\,t_2)-f(q_1,\,t_1) \end{equation*}

最后两项是常数，它们将在变分时消失，从而L和L'给出的拉格朗日方程完全一致。这就是说，在拉格朗日函数中可以肆意添加这样的函数f而不会对其描述的力学过程产生任何改变。

现在，我们可以继续“猜测”自由质点的拉格朗日函数了。假设存在两个惯性系K和K'，它们之间相差一个无穷小速度\boldsymbol{\varepsilon}。若在K中质点的拉格朗日函数为L(v^2)，则在K'中，

(5)   \begin{equation*} L'=L(v^2+\boldsymbol{v}\cdot\boldsymbol{\varepsilon}+\varepsilon^2) \end{equation*}

若将其展开并舍弃高阶项，就有：

(6)   \begin{equation*} L'=L(v^2)+2\frac{\partial L}{\partial v^2}\boldsymbol{v}\cdot\boldsymbol{\varepsilon} \end{equation*}

因L和L'描述的同一物理过程而只有参考系的区别，因此其拉格朗日方程因给出同类的解，故而它们之间只能相差一个时间的全导数。为了达到这一点，只有\frac{\partial L}{\partial v^2}是常数。因此不妨有：

(7)   \begin{equation*} L=\frac{1}{2}mv^2 \end{equation*}

其中m为常数，称为质量。

进一步，我们可以考虑封闭质点系的拉格朗日函数。封闭质点系与自由质点除了质点数目之外的唯一区别是，质点与质点之间可能存在相互作用。一般情况下，这类相互作用只与质点间的相对距离有关。因此，一个想法是在拉格朗日函数之间添加一项-U，它只和质点的相对距离有关。从而封闭质点系的拉格朗日函数可以写为：

(8)   \begin{equation*} L=\sum_i\frac{1}{2}m_iv_i^2-U \end{equation*}

一般地，第一项称为动能，第二项称为势能。当然，除了使用笛卡尔坐标外，也能使用更方便的广义坐标，此时只需要做如下变量替换即可：

(9)   \begin{equation*} \left\{ \begin{split} \boldsymbol{r_i}&=\boldsymbol{r_i}(q_1,\,q_2,\,...,\,q_n)\\ \boldsymbol{v_i}&=\sum_j\frac{\partial\boldsymbol{r_i}}{\partial q_j}(q_1,\,q_2,\,...,\,q_n)\dot{q_j}\\ \end{split} \right. \end{equation*}

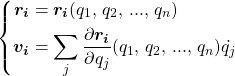
以上是对封闭质点系的拉格朗日函数的讨论。但在实际工作中，一般很难考虑一个完整的封闭系统，比如在计算卫星轨道时，总不希望把地球的运动也一并考虑进去吧。因此，我们需要看看非封闭质点系的拉格朗日函数。事实上也很简单。记需要研究的开放系统为A，它与另一个开放系统B共同构成封闭系统。那么，它们共同的拉格朗日函数可以写为：

(10)   \begin{equation*} L=\sum_i\frac{1}{2}(m_{Ai}v_{Ai}^2+m_{Bi}v_{Bi}^2)+U(\boldsymbol{r_{A1}},\,...,\,\boldsymbol{r_{An}},\,\boldsymbol{r_{B1}},\,...,\,\boldsymbol{r_{Bn}}) \end{equation*}

一般来讲，B的运动是完全已知的（否则它就是问题的一部分了），因此B的动能成为时间的全导数，可以略去。因此A的拉格朗日函数为：

(11)   \begin{equation*} L=\sum_i\frac{1}{2}m_{Ai}v_{Ai}^2+U(\boldsymbol{r_{A1}},\,...,\,\boldsymbol{r_{An}},\,t) \end{equation*}

可见，其与封闭系统的拉格朗日函数的区别仅有势能中可能显含时间。以上推导对于使用广义坐标表示的情况也是成立的。

到目前为止，我们有了具体形式的拉格朗日函数。可以看到，在给出的过程中，存在大量物理上的假设（“俺寻思”）。但作为一个理论的基础也并无不可。当然，或许看上去这条路没有从牛顿力学出发得到拉格朗日力学的路径清晰和“严谨”，但就我个人的审美而言，我还是更偏好于朗道这样给出的路，提供了一个更高更妙更全面更“公理化”的视点。那么下一篇，就是各守恒量的导出了。