关于量子力学的表象

发布于 2021-01-10  94 次阅读

作者按：本文原本的写作目的在于，从形式理论出发重新看待量子力学的一些公式，以期在一些问题上获得更加明确的认识；写作动机在于，之前考研复习量子力学的时候，复习参考书从中间的某章开始讨论形式理论，同时没有专门就前面的章节与本章之间的衔接做探讨。这种撕裂感和非演绎感让我感到十分不适。然而，在本文写作过程中，作者意识到，要想从演绎的、数学的角度构建形式理论并不是一个十分容易的工作；同时，在本文尚未完成时，研究生考试就已结束。因此，在继续了一段时间的思考后，重新写作本文，以期获得更好的效果。限于作者水平，本文只讨论离散谱的情形。

一. 我们所考虑的问题

先考虑一个一维无限深方势阱中的粒子，初学量子力学时，可能会直接使用如下的薛定谔方程：

(1)   \begin{equation*} (-\frac{\hbar^2}{2m}\nabla^2+V(x))\psi=\frac{\partial \psi}{\partial t} \end{equation*}

用分离变量法解出所谓的本征函数\psi_n(x)，然后将初态的波函数用本征函数展开，再乘上含时因子，以看到系统是如何随时间演化的。

从更抽象的角度看，我们是做了什么呢？我们的目的是知道系统的在初态，比如记作\psi的态，下如何演化。为了看到这一点，我们找到了一组态，它们是如何随时间变化是我们已经知晓的。然后，我们说\psi这个态可以以某种方式表达为这一组态的叠加，从而知晓\psi如何随时间演化。

但是，这里的问题是，(1)为什么这组态的叠加可以代表另外的态？(2)为什么任何一个态可以表达为这组态的某种加和？(3)我们要怎么知道某个态如何表示为某组态的叠加？

二. 第一个问题

第一个问题是很好解答的，它的答案基于量子力学的态叠加原理。但表述态叠加原理之前，我们还需要一点准备。

我们需要考虑这样一个集合H，集合的元素，这里记作\psi^a（稍后会看到这种记法的意义），是我们考虑的一个量子力学系统中的某个态。那么，态叠加原理是说，对于属于这个集合的可数个态(\psi_i)^a，它们的线性组合\sum_i c_i(\psi_i)^a也属于这个集合，其中c_i\in C。用更数学的语言说，态叠加原理定义了H上的数乘和加法；而物理上的要求则保证了交换律和结合律的成立。因此可以说，态叠加原理使得H成为了线性空间（向量空间）。

这样，H中的元素\psi^a就被称作一个向量。而任意个向量的线性组合依然是H中的元素，这就解决了第一个问题。

但是，或问，从量子力学的经验来看，如果\psi^a是一个态，那么c\psi^a, c\in C应该也是相同的态，这似乎和直觉上的向量空间不相符合。首先，如果定义数乘是这样一个映射：

(2)   \begin{equation*} \begin{split}C\times H \to H\\ c\times \psi^a\mapsto \psi^a\\ \end{split} \end{equation*}

那么于线性空间上的定义也毫无问题；其次，尽管物理上二者是一个相同的态（因为它们有相同的行为），但是在数学上，将其作为不同的态也无伤大雅。同时，这样的处理方式也废除了波函数归一化的要求——事实上，波函数的归一化只有实际计算中的意义，归一化系数在形式理论的讨论中是无关紧要的。总的来说，我们看到，态叠加原理使得一个量子系统所有可能的量子态组成的集合成为了线性空间，一个量子态就是线性空间中的一个矢量。这样，就允许我们把线性空间的全部定理，一股脑的全倒在量子力学上面。

三. 第二个问题

那么，接下来的问题是，为什么任何一个量子态都能表示为其他量子态的加和？一个很trivial的情况是，任意一个量子态当然可以表示为它本身的加和：\psi^a=1\times\psi^a。更一般的说，假设某个量子态\psi^a不能表示为任意量子态的加和，那么，从线性空间中任意选择一个量子态\varphi^a，那么，\psi^a+\varphi^a一定不是线性空间的元素，因为如果它是线性空间的某个元素\alpha^a的话，就有\psi^a=-\varphi^a+\alpha^a，这与假设矛盾；但是，如果这样的话，H就不是线性空间了。因此，通过反证法就可以看出，任意一个量子态都能表示为其他量子态的加和。

当然，这样一个存在性的证明并不能让我们满意。在这一基础上，我们更想知道第三个问题：如何将某个态表示为其他态的叠加？

四. 第三个问题

通过线性代数的知识，我们知道线性空间H可以由可数个元素(\psi_i)^a张成，这些元素线性无关。即，对任意H的元素\phi^a，有\phi^a=\sum_ic_i(\psi_i)^a，其中c_i\in C且不全为0.因此，一个问题就是，对于给定的\{(\psi_i)^a\}和\phi^a，如何求出c_i。

要考虑这个问题，就要引入内积的概念。这里存在两种方式，第一种是将内积定义为一个从H\times H到C的映射f，它满足：

(3)   \begin{equation*} f((\psi_i)^a,\hspace{1ex}(\psi_j)^a)=\delta_{ij} \end{equation*}

(4)   \begin{equation*} f(\psi^a,\hspace{1ex}\phi^a)=f(\phi^a,\hspace{1ex}\psi^a)^*\end{equation*}

和

(5)   \begin{equation*} f(\sum_ic_i(\phi_i)^a,\hspace{1ex}\psi^a)=\sum_ic_i^*f((\phi_i)^a,\hspace{1ex}\psi^a)\end{equation*}

可以证明它和通常接触到的内积的定义一致。因此容易得到c_i=f(\phi^a,\hspace{1ex}(\psi_i)^a)。可以看出，f(\cdot,\hspace{1ex}\cdot)中，第一个\cdot处就是所谓的左矢，第二个就是所谓的右矢。

而第二种方式，则需要稍微绕一下远路。但它却揭示了更多的东西。

从H出发，我们可以定义所谓的对偶空间H^*。我们定义，对偶空间H^*的元素\psi_a是一个从H到C的线性映射，即：

(6)   \begin{equation*} \psi_a(\sum_ic_i\phi^a)=\sum_ic_i\psi_a(\phi^a) \end{equation*}

再定义加法和数乘：

(7)   \begin{equation*} (\psi_a+\phi_a)(\beta^b)=\psi_a(\beta^b)+\phi_a(\beta^b) \end{equation*}

(8)   \begin{equation*} (\lambda\psi_a)(\phi^b)=\lambda(\psi_a(\phi^b)) \end{equation*}

这样就能证明H^*是线性空间。可以看到，H^*是依托于H的，其具体结构依赖于上述映射的具体形式。我们任意选一个从{\psi_i}^a到H的一一映射，记映射的像为{(\psi^i)_a}。然后，让(\psi^i)_a((\psi_j)^b)=\delta^j_i。可以证明，{\psi^i}_a构成了H^*的一组基。

通过这种方式，我们就得到了H^*中任意一个元素\psi_a是如何作用于H中的元素\phi^b：

(9)   \begin{equation*} \begin{split} \psi_a(\phi^b) & =\sum_ia_i(\psi^i)_a(\sum_jb_j(\phi_j)^b) \\ & =\sum_{i,j}a_ib_j(\psi^i)_a((\phi_j)^b)\\ & =\sum_ia_ib_i\\ \end{split} \end{equation*}

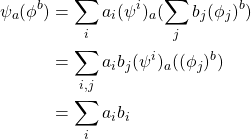
根据线性代数的知识，我们知道，两个维度相同的线性空间是同构的。我们可以定义一个从H到H^*的同构映射f。这个同构映射的选取相当任意，但一个自然的选取方式是

(10)   \begin{equation*} \begin{split} H & \to H^*\\ \sum_ic_i(\psi_i)^a & \mapsto \sum_i(c_i)^*(\psi^i)_a\\ \end{split} \end{equation*}

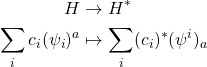
建立了同构映射，我们终于可以定义内积了。所谓\psi^a和\phi^a内积，即是f(\psi^a)\phi^a。其值可以很容易的计算出来。而今后，这样的内积（更一般的说，对偶空间对原空间的作用）简记为\psi_a\phi^a。有了内积的定义，再按第一条路就能容易的得到c_i。

容易看到，所谓对偶空间，其实就是左矢的集合；而空间H，就是右矢的集合。而量子力学的那一套运算，就可以建立在空间和对偶空间上的运算，特别是张量积运算上。譬如，所谓的完备性关系，实际上就是：\psi^a\psi^b=\delta^{ab}；同样的可以证明，任意一个（离散谱的）算符，都对应于H上的一个二阶张量A^{ab}，选取A^{ab}表象的过程，就是选择它特征矢量作为H的基矢的过程，等等。篇幅所限，不再赘述。总之，可以看到，建立在这上面的量子力学的数学基础，很有味道。