在上一篇文章中,我们通过构建自然数上的等价关系,给出等价关系对应的分割,并通过定义整数集合就是这些分割的方式,从自然数构造出了整数。我们看到,整数与从自然数加法、乘法推广得到的整数上的加法与乘法一起构成了一个环。作为一个环,整数内有加法逆元,但是没有乘法逆元。这很好,但不完全好。如果能在向整数里面引入乘法逆元,将其扩张成一个域,就再好不过了。这样做的结果就是,我们能抵达有理数。
首先来看看域的定义。一个集合![]() 配合其上的封闭运算加法和乘法
配合其上的封闭运算加法和乘法![]() 被称为域,当且仅当:
被称为域,当且仅当:
(1) 对于加法,有A. 恒元0;B. 交换;C. 结合律;D. 可逆 ;
(2) 对于乘法,有A. 幺元1且![]() ;B. 交换;C. 结合律;D.除恒元外可逆;
;B. 交换;C. 结合律;D.除恒元外可逆;
(3) 乘法对加法满足分配律。
简单的说即:(1)含幺交换环;(2)![]() ;(3)非零元可逆。对照整数上的加法和乘法,可以看见,关键是要引入乘法逆元。那么,类比我们引入加法逆元的过程,我们应当也能按照类似的做法,在
;(3)非零元可逆。对照整数上的加法和乘法,可以看见,关键是要引入乘法逆元。那么,类比我们引入加法逆元的过程,我们应当也能按照类似的做法,在![]() 上针对乘法构造一个等价关系,并将有理数集定义为
上针对乘法构造一个等价关系,并将有理数集定义为 ![]() 对这个等价关系的商集,最终证明有理数集满足域的公理,是一个合格的域。
对这个等价关系的商集,最终证明有理数集满足域的公理,是一个合格的域。
一. 有理数集的构造
从经验上说,一个有理数能表示成![]() 的形式,这里
的形式,这里![]() 。因此我们考虑定义集合
。因此我们考虑定义集合![]() 上的加法和乘法如下:
上的加法和乘法如下:
加法:![]() ;
;
乘法:![]() 。
。
类似的,在不引起混淆的情况下,后文中的加号和乘号都省略。通过上述方法定义的加法和乘法满足交换律和结合律,这一点可以通过![]() 上加法和乘法的各运算律导出来。鉴于乘法的交换律和结合律极其显然,这里就以加法为例好了:
上加法和乘法的各运算律导出来。鉴于乘法的交换律和结合律极其显然,这里就以加法为例好了:
(1) 交换律:
(1) ![]()
(2) 结合律:
(2) ![]()
可惜的是,目前为止乘法对加法的分配律还不能成立。不过这并不重要,因为这还只是![]() 上的运算而已,距离
上的运算而已,距离![]() 还有一段距离。接下来我们定义引入乘法逆元所需要的等价关系:
还有一段距离。接下来我们定义引入乘法逆元所需要的等价关系:
等价关系:若![]() ,且
,且![]() ,则称
,则称![]() 与
与![]() 等价,记作
等价,记作![]() 。
。
这样的定义是合理的,接下来我们就来验证合理性。
(1) 自反性:显然,![]() ,都有
,都有![]() ,所以
,所以![]() ;
;
(2) 对称性:![]() ,若
,若 ![]() ,则
,则![]() ,从而
,从而![]() ,于是
,于是![]() ;
;
(3) 传递性:![]() ,若
,若![]() ,
,![]() ,则:
,则:
(3) ![]()
而![]() ,从而
,从而![]() ,于是
,于是
(4) ![]()
故而![]() 。
。
因此上述定义得到的关系确实是一个等价关系。关于这个等价关系,我们能够看到一个很有趣的性质:若![]() ,
,![]() ,那么
,那么![]() ,这是显然的。这个性质将帮助我们证明乘法对加法的分配律的成立。
,这是显然的。这个性质将帮助我们证明乘法对加法的分配律的成立。
那么,类似于我们之前所做的,就可以得到![]() 对这个等价关系的分拆。这些等价类的集合就是我们所希望得到的有理数集
对这个等价关系的分拆。这些等价类的集合就是我们所希望得到的有理数集![]() 。接下来,我们就来证明在这个
。接下来,我们就来证明在这个![]() 上加法和乘法都满足域的公理,使得它成为一个域。
上加法和乘法都满足域的公理,使得它成为一个域。
二. 从有理数集到有理数域
首先是![]() 上的运算。类似于之前的操作,我们定义等价类之前的运算就是代表元之间进行运算:
上的运算。类似于之前的操作,我们定义等价类之前的运算就是代表元之间进行运算:![]() :
:
(1) 加法:![]() ;
;
(2) 乘法:![]() 。
。
首先,我们来验证这样的定义是合理的。对于加法:
若![]() ,
,![]() ,
,![]() 是
是![]() 的两个不同代表元,
的两个不同代表元,![]() 是
是![]() 的代表元,那么:
的代表元,那么:
(5) ![]()
(6) ![]()
此时,因为![]() 有:
有:
(7) ![]()
从而两代表元是等价的,因此加法的定义是合理的。对于乘法:
(8) ![]()
(9) ![]()
因此有![]() ,从而两等价元等价,因此乘法的定义也是合理的。
,从而两等价元等价,因此乘法的定义也是合理的。
1. 运算律
根据加法和乘法的定义,有理数集上加法和乘法各自的交换律和结合律是显然的。那么剩下的运算律就是分配律了。我们现在就来证明分配律。
考虑三个等价类![]() ,
,![]() ,
,![]() ,有:
,有:
(10) ![]()
由于![]() ,而
,而
(11) 
上述证明反之亦然,从而乘法对加法的分配律是成立的。接下来,我们来看看加法和乘法的恒元和逆元。
2. 恒元与逆元
注意到我们如此定义运算的动机,我们可以考虑如下的等价类:![]() ,可以看到,对于加法,他满足:
,可以看到,对于加法,他满足:
(12) ![]()
更一般的,对于![]() 内的任意代表元
内的任意代表元![]() ,都有:
,都有:
(13) ![]()
可见,对于加法,其恒元为![]() 。类似的,对于乘法,考虑
。类似的,对于乘法,考虑![]() ,有:
,有:
(14) ![]()
因此,乘法的幺元即是![]() 。
。
对于逆元,则可以容易的验证,对元素![]() ,加法的逆元是
,加法的逆元是![]() ,(若
,(若![]() )乘法逆元是
)乘法逆元是![]() 。逆元的验证就留给读者了。
。逆元的验证就留给读者了。
综合上述证明,我们看到,集合![]() 确实满足作为域的各项性质。因此我们知道,
确实满足作为域的各项性质。因此我们知道,![]() 的确是域。
的确是域。
三. 作为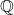 的子集的
的子集的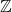
在之前的文章中,我们并没有详细讨论为何用“下级”集合构造出的“上级”的集合包含“下级”的集合并将其作为子集,同时“上级”集合中的运算为何与“下级”集合中的运算保持一致。现在,借着我们终于抵达了域这一级代数结构的机会,我们来详细讨论一下这个问题。
目前为止,在这里定义的![]() 与
与![]() 并不存在任何的包含关系。这是因为二者的元素根本就不一样:
并不存在任何的包含关系。这是因为二者的元素根本就不一样:![]() 的元素是对集合
的元素是对集合![]() 的分拆,而
的分拆,而![]() 的元素则是
的元素则是![]() 的分拆。可以说,前者的元素是后者的有序对的集合。因此,二者并不存在任何的包含关系。但是,在数学中,我们经常使用“
的分拆。可以说,前者的元素是后者的有序对的集合。因此,二者并不存在任何的包含关系。但是,在数学中,我们经常使用“![]() 是
是![]() 的子集”这样的述语。这样的述语是对的吗?自然也是对的,不过要看到这句述语的正确性,我们还要往前走一小步。
的子集”这样的述语。这样的述语是对的吗?自然也是对的,不过要看到这句述语的正确性,我们还要往前走一小步。
考虑![]() 的子集
的子集![]() 。显然,在
。显然,在![]() 与
与![]() 之间存在一个一一对应的关系:
之间存在一个一一对应的关系:![]() 。如果我们进一步考察
。如果我们进一步考察![]() 上的运算,就能看到:
上的运算,就能看到:
(15) ![]()
(16) ![]()
于是我们可以证明![]() 这个映射具有保运算的特征,简单的说即
这个映射具有保运算的特征,简单的说即![]() ,
,![]() 。因此
。因此![]() 和
和![]() 是同构的。既然是同构的,那么它们都可以认为是整数环的一种表示。因此我们把前者认作新的整数环,而把后者“忘记”。这样,我们就能看到,
是同构的。既然是同构的,那么它们都可以认为是整数环的一种表示。因此我们把前者认作新的整数环,而把后者“忘记”。这样,我们就能看到,![]() 的确是
的确是![]() 的子集,同时还保持了所有的”旧“整数环的性质。在之前和之后的文章中,我们都遇到过或将再次遇到这样的问题,解决方法也都是类似的,即在新的集合中找出与旧集合同构的部分。
的子集,同时还保持了所有的”旧“整数环的性质。在之前和之后的文章中,我们都遇到过或将再次遇到这样的问题,解决方法也都是类似的,即在新的集合中找出与旧集合同构的部分。
四. 回归到通常的记号
那么,实际上整个有理数域![]() 就已经构造完成了,但这与通常的记法还有一些区别,毕竟实际使用中没人把一个有理数写成
就已经构造完成了,但这与通常的记法还有一些区别,毕竟实际使用中没人把一个有理数写成![]() 。因此,我们将引入下列记号,来使整个记号系统回归到通常使用的形式上。
。因此,我们将引入下列记号,来使整个记号系统回归到通常使用的形式上。
记号1:乘法的幺元![]() 记作
记作![]() ,加法的恒元
,加法的恒元![]() 记作
记作![]() ;
;
记号2:![]() ,
,![]() ,将
,将![]() 记作
记作![]() ,或
,或![]() ;
;
记号3:若![]() ,即
,即![]() ,则将
,则将![]() 简记为
简记为![]() 。
。
注意到,![]() ,都有:
,都有:
(17) ![]()
那么,按照上述记号,就有![]() 。可见,这就回到了我们熟悉的“一个有理数总能表示成两个整数之商”的形式,一个有理数就能用这样的分数的形式表示出来。而一个有理数的各种(非最简)分数的表示,如
。可见,这就回到了我们熟悉的“一个有理数总能表示成两个整数之商”的形式,一个有理数就能用这样的分数的形式表示出来。而一个有理数的各种(非最简)分数的表示,如![]() ,
,![]() ,
,![]() ……等等,实际上都是代表元选取的不同的结果。当然,我们可以在整数环上引入互质的概念,从而给出一个选取代表元的方案,不过这和本文的主题稍有偏离,因此就略去了。此外,我们还能轻易看到这套记号系统与之前定义的运算规则的一致性,这里当然也略过不谈,毕竟太简单了。
……等等,实际上都是代表元选取的不同的结果。当然,我们可以在整数环上引入互质的概念,从而给出一个选取代表元的方案,不过这和本文的主题稍有偏离,因此就略去了。此外,我们还能轻易看到这套记号系统与之前定义的运算规则的一致性,这里当然也略过不谈,毕竟太简单了。
五. 有理数域的序
在结束本文之前,我们还要引入一个在之前并没有得到过多重视的概念:序。虽然这个概念很简单,但从有理数域开始,序的概念就逐渐重要了起来,首当其冲的就是在下一节中我们将看到,序对我们引出实数域有着非常重要的作用。
一个集合![]() 上的“序”是一种关系,通常被记作
上的“序”是一种关系,通常被记作![]() ,他满足:
,他满足:
(1) ![]() ,
,![]() ,
,![]() ,
,![]() 中有且仅有一个成立;
中有且仅有一个成立;
(2) ![]() ,若
,若![]() ,
,![]() ,则
,则![]() 。
。
在自然数集上,序可以简单的定义:![]() ,若
,若![]() ,使得
,使得![]() ,则称
,则称![]() 。首先,我们来证明上述定义的关系满足序的条件:
。首先,我们来证明上述定义的关系满足序的条件:
首先,若![]() ,那么若存在
,那么若存在![]() 使得
使得![]() ,那么根据加法的定义,我们看到对
,那么根据加法的定义,我们看到对![]() 做
做![]() 次后继运算就能得到
次后继运算就能得到![]() ,而
,而![]() ,于是(1)若
,于是(1)若![]() ,那么就违反了PA3:0不是任何数的后继;(2)若
,那么就违反了PA3:0不是任何数的后继;(2)若![]() ,那么就违反了PA4:不同自然数的后继不同,即第
,那么就违反了PA4:不同自然数的后继不同,即第![]() 个自然数和第
个自然数和第![]() 个自然数有相同的后继,除非这两个自然数也相同。类似的,就得到第
个自然数有相同的后继,除非这两个自然数也相同。类似的,就得到第![]() 个自然数与
个自然数与![]() 个自然数相同、第
个自然数相同、第![]() 个自然数与
个自然数与![]() 个自然数相同……直到第
个自然数相同……直到第![]() 个自然数与0相同,即
个自然数与0相同,即![]() ,这与假设矛盾。因此
,这与假设矛盾。因此![]() 与
与![]() 不能同时成立;类似的,我们可以得到
不能同时成立;类似的,我们可以得到![]() 与
与![]() 不能同时成立。
不能同时成立。
其次,若![]() ,那么必定存在
,那么必定存在![]() ,使得
,使得![]() 成立或者
成立或者![]() 成立。这是因为,如果不存在这样的
成立。这是因为,如果不存在这样的![]() 使得上述命题成立,那么就说明既不能由
使得上述命题成立,那么就说明既不能由![]() 出发通过后继运算得到
出发通过后继运算得到![]() ,也不能由
,也不能由![]() 出发由后继运算得到
出发由后继运算得到![]() 。那么,我们考虑这样两个集合
。那么,我们考虑这样两个集合![]() 和
和![]() ,其中,
,其中,![]() ,即由
,即由![]() 开始通过后继运算直到
开始通过后继运算直到![]() 的集合。因为不能由
的集合。因为不能由![]() 不断做后继运算得到
不断做后继运算得到![]() ,因此
,因此![]() ;
;![]() ,即
,即![]() 的后继、后继的后继……构成的集合,显然
的后继、后继的后继……构成的集合,显然![]() ,否则就能由
,否则就能由![]() 做后继运算得到
做后继运算得到![]() 。这样,
。这样,![]() ,但根据数学归纳法,
,但根据数学归纳法,![]() ,因此
,因此![]() ,这就有了矛盾。因此,命题成立。
,这就有了矛盾。因此,命题成立。
再次,若![]() ,那么
,那么![]() 和
和![]() 只有一个成立。这是因为,若存在
只有一个成立。这是因为,若存在![]() 使得
使得![]() 且
且![]() ,那么就存在
,那么就存在![]() 使得
使得![]() 和
和![]() ,即
,即![]() ,这就违反了PA4.
,这就违反了PA4.
因此,序的要求中第一条就被满足了。第二条则是显然的,同样留给读者自己去思考了。这样,我们就在![]() 上定义了序关系。
上定义了序关系。![]() 上的序关系更简单:
上的序关系更简单:![]() ,若
,若![]() ,那么
,那么![]() 。在整数群的群的结构的帮助下,证明上述定义符合要求更加简单。
。在整数群的群的结构的帮助下,证明上述定义符合要求更加简单。
那么,我们现在就来到了有理数域上的序。有理数上的序由整数集上的序诱导得到:若![]() ,
,![]() ,
,![]() ,那么
,那么![]() 定义为
定义为![]() ,后者中的序关系是整数集上的序关系。上述定义满足序的条件(1)是显然的。对于条件(2),若
,后者中的序关系是整数集上的序关系。上述定义满足序的条件(1)是显然的。对于条件(2),若![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,那么有
,那么有![]() ,
,![]() ,从而(1)若
,从而(1)若![]() ,那么
,那么![]() ,又
,又![]() ,故
,故![]() ,而
,而![]() ,故
,故![]() ;(2)若
;(2)若![]() ,则
,则![]() ,又
,又![]() ,从而
,从而![]() ,故
,故![]() ;(3)若
;(3)若![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,自然有
,自然有![]() 。从而我们看到,上述的关系的确是有理数上的序。这样,有理数域就成为了有序域。
。从而我们看到,上述的关系的确是有理数上的序。这样,有理数域就成为了有序域。
在以上的讨论中,虽然我们只定义了![]() 符号,但
符号,但![]() 、
、![]() 、
、![]() 都能十分容易的根据
都能十分容易的根据![]() 定义出来,如
定义出来,如![]() 是:若
是:若![]() ,那么
,那么![]() 。
。
有序域的概念十分重要,我们马上就会看到。不过,在这里,还可以插入一条定理,它是有理数域和之前的整数集、自然数集等之间的一个十分重要的区别。这条定理是说,若![]() 且
且![]() ,那么
,那么![]() ,使得
,使得![]() 。这个定理这里不打算证明,但聪明的读者应该知道如何构造。
。这个定理这里不打算证明,但聪明的读者应该知道如何构造。
六. 有理数域的局限性:我们为什么需要实数域
那么最后,作为一个承上启下、引出下一篇文章的引子,我们来谈谈有理数域的局限。首先,众所周知的是,有理数域不具有代数完备性。也就是说,对于有理数域上的任意多项式方程,不是每一个方程都在有理数域内有根的。然而,虽然要在下一篇文章中才谈到,但实际上可以先在这里提一下,即实数域也并不是代数完备的。为了解决代数完备性的问题,我们必须要走进复数域中。因此,实数域并不是解决代数完备性问题的最终答案,而只是其中的一站而已。
其次,也是由上述问题进一步揭示的,有理数域并不具有最小上界性。
最小上界性是指,对一个非空集合
,若
,
,使得(1)
,
(即
是
的上界);(2) 若
,则
,使得
(即
不是
的上界),此时称
具有最小上界性。
可以随意举一个例子来验证有理数域不具有最小上界性。这里引用Rudin的一个例子:考虑所有满足![]() 的正有理数构成的集合
的正有理数构成的集合![]() 和
和![]() 的正有理数构成的集合
的正有理数构成的集合![]() 。
。![]() ,考虑
,考虑
(18) ![]()
(19) ![]()
那么若![]() ,那么
,那么![]() ,
,![]() ;而由最后一个式子可见
;而由最后一个式子可见![]() ,故
,故![]() 。因此在
。因此在![]() 中不存在
中不存在![]() 的上界。若
的上界。若![]() ,那么类似有
,那么类似有![]() ;而最后一个式子说明
;而最后一个式子说明![]() ,故
,故![]() ,因此在
,因此在![]() 中虽然存在
中虽然存在![]() 的上界,但是不存在最小上界。因此
的上界,但是不存在最小上界。因此![]() 没有最小上界。可见
没有最小上界。可见![]() 不存在最小上界性。同样借用Rudin的话,“
不存在最小上界性。同样借用Rudin的话,“![]() 中不具有最小上界性说明虽然
中不具有最小上界性说明虽然![]() 是稠密的,但依然存在一些空隙”。要填补这些空隙,就是实数集的任务了。也正因如此,实数集虽然不具有代数完备性,但也是数学,特别是分析学的核心。那么,下一篇文章,我们就来讲讲如何构造实数集。
是稠密的,但依然存在一些空隙”。要填补这些空隙,就是实数集的任务了。也正因如此,实数集虽然不具有代数完备性,但也是数学,特别是分析学的核心。那么,下一篇文章,我们就来讲讲如何构造实数集。





Comments NOTHING